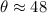Answer:

Since the angle between the two vectors is not 180 or 0 degrees we can conclude that are not parallel
And the anfle is approximately
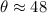
Explanation:
For this case first we need to calculate the dot product of the vectors, and after this if the dot product is not equal to 0 we can calculate the angle between the two vectors in order to see if there are parallel or not.
a=[1,2,-2], b=[4,0,-3,]
The dot product on this case is:
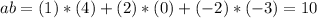
Since the dot product is not equal to zero then the two vectors are not orthogonal.
Now we can calculate the magnitude of each vector like this:

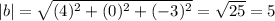
And finally we can calculate the angle between the vectors like this:
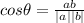
And the angle is given by:
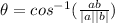
If we replace we got:

Since the angle between the two vectors is not 180 or 0 degrees we can conclude that are not parallel
And the anfle is approximately