Question

Present Value  A real estate investment is expected to produce a uniform continuous rate of money flow of $8000 per year for 6 years. Find the present value at the following rates, compounded continuously.

a. 2%
b. 5%
c. 8%

Answer 1

To determine the present value at the rate r, compounded continuously we have

P= Ae-rt

where

P = Present value

A=amount = $8000

r=interest rate

t=time taken = 6years

dP = 8000
`\int\limits^6_0 {e-rt} \, dt`

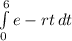
a) So now for r = 2% = 0.02, we have

dP = -8000(e-0.02t
`\left \{ {{t=6} \atop {t=0}} \right.`)

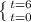dP = -8000 (e-3/25 - 1) = -8000 (-0.1131)

dP = $905 at 2%

b) for r = 5% = 0.05, we have

dP = -8000(e-0.05t
`\left \{ {{t=6} \atop {t=0}} \right.`)

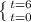dP = -8000 (e-3/10 - 1) = -8000 (-0.2592)

dP = $2074 at 5%

c) for r = 8% = 0.08, we have

dP = -8000(e-0.08t
`\left \{ {{t=6} \atop {t=0}} \right.`)

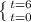dP = -8000 (e-12/25 - 1) = -8000 (-0.3812)

dP = $3050 at 8%

Answer 2

a. $42,572 at 2%,

b. $35,559 at 5%

c. $29,702 at 8%

Explanation:

The formula used for FV calculation for Continuous Compounding is as under:

`FV = PV e^(i * t)`

Where,

FV = Future Value = $8000 each year (At the end of 6 years = $8000 x 6 = $48,000)

PV = Present Value

e = Mathematical Constant = 2.713

i = Interest Rate

t= time in years

a) For 2%:

`FV = PV e^(i * t)\\48000 = PV e^(0.02 * 6)\\48000 = 1.1275 (PV)\\PV = 42,572`

b) For 5%:;

`FV = PV e^(i * t)\\48000 = PV e^(0.05 * 6)\\48000 = 1.35 (PV)\\PV = 35,559\\`

c) For 8%:

`FV = PV e^(i * t)\\48000 = PV e^(0.08 * 6)\\48000 = 1.616 (PV)\\PV = 29,702`

Note: Investing $42,572 at 2%, $35,559 at 5% and $29,702 at 8% today will get $48,000 at the end of 6 years.