Question

find the angle between the vectors. (first find the exact expression and then approximate to the nearest degree. ) a=[0,1,1]. B=[1,2,-3]

Answer 1

Angle between the given vectors is approximately 100.89 degrees.

Explanation:

We are given the following in the question:

`a=[0,1,1], B=[1,2,-3]`

We have to find angle between the two vectors.

First we evaluate the dot product for the given vectors.

`a.b = (0.1) + (1.2) + (1.-3) \\=-1`

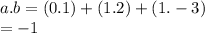
The magnitude of the vectors can be calculated in the following manner

`|a| = √(0^2 + 1^2 + 1^2) = √(2)\\|b| = √(1^2 + 2^2 + (-3)^2) = √(14)`

Formula:

`a.b = |a| |b| \cos \theta\\\text{where theta is the angle between the two vectors}`

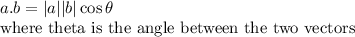
Putting the values, we get,

`-1 = (\sqrt2)(√(14))\cos \theta\\\\\cos \theta = \displaystyle(-1)/(2\sqrt7)\\\\\theta = \arccos((-1)/(2\sqrt7))\\\\\theta \approx  1.76\text{ radians}\\\theta \approx 100.89\text{ degrees}`

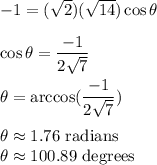
Angle between the given vectors is approximately 100.89 degrees.