Answer:
a)
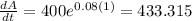
b)
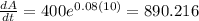
c)

Explanation:
For this case we have the following expression for the balance:

And we are interested on the rate at which the balance is changing for some values of t. The correct way to answer this is finding the derivate respect to t of A like this:
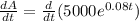
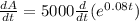
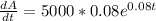
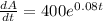
So then we can solve for the different years like this
Part a
t= 1 years
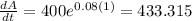
So on this case would be $433.315 dollars per year
Part b
t=10 years
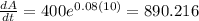
So on this case would be $890.216 dollars per year
Part c
t=50 years

So on this case would be $21839.260 dollars per year