Question

The function in Exercise represents the rate of flow of money in dollars per year. Assume a 10-year period at 8% compounded continuously and find the following: (a) the present value; (b) the accumulated amount of money flow at t=10.

f(t)=0.01t+100

Answer 1

a) The present value is 688.64 $

b) The accumulated amount is 1532.60 $

Explanation:

a) The preset value equation is given by this formula:

`P=\int^(T)_(0)f(t)e^(-rt)dt`

where:

• T is the period in years (T = 10 years)
• r is the annual interest rate (r=0.08)

So we have:

`P=\int^(T)_(0)(0.01t+100)e^(-rt)dt`

Now we just need to solve this integral.

`P=\int^(T)_(0)0.01te^(-rt)dt+\int^(T)_(0)100e^(-rt)dt`

`P=e^(-0.08t)(-1.56-0.13t)|^(10)_(0)+1250e^(-0.08t)|^(10)_(0)`

`P=0.30+688.34=688.64 $`

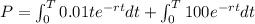
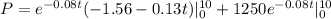
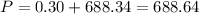
The present value is 688.64 $

b) The accumulated amount of money flow formula is:

`A=e^(r\tau)\int^(T)_(0)f(t)e^(-rt)dt`

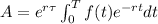
We have the same equation but whit a term that depends of τ, in our case it is 10.

So we have:

`A=e^(r\tau)\int^(T)_(0)(0.01t+100)e^(-rt)dt=e^(0.08\cdot 10)P`

`A=e^(0.08\cdot 10)688.64=1532.60 $`

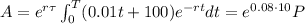
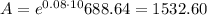
The accumulated amount is 1532.60 $

Have a nice day!