Question

Probability In a recent year,the mean SAT score for college-bound seniors on the mathematics portion was 516,with a standard deviation of 116.

(a) Assuming the date can be modeled by a normal probability density function,find a model for these data.
(b) Use a graphing utility to graph the model.Be sure to choose an appropriate viewing window.
(c) Find the derivative of the model.
(d) show that f' > 0 for x < µ and f' < 0 for x > µ.

Answer 1

a)
`f(x) = (1)/(√(2\pi)(116)) e^{-(1)/(2) ((x-516)/(116))^2}`

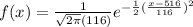
b) We can use the following R code to plot the density function:

> x<-seq(0,1000,by=0.1)

> y=dnorm(x,mean=516,sd=116)

> plot(x,y,main="Density plot")

And the result is on the figure attached

c)
`(d)/(\d \mu) = (1)/(√(2\pi) \sigma) e^{-(1)/(2) ((x-\mu)/(\sigma))^2} * ((\mu-x)/(\sigma)) *((1)/(\sigma))`

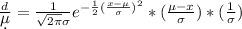
d) For this case if we analyze the function obtained for
`(d)/(d\mu)` we can see that if we replace any value of
`x < \mu` , and we know that
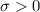`\sigma>0` always then we will have a positive value since we just need to analyze this part of the expression :

`(\mu-x)/(\sigma)`

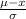
And when we replace any value
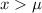`x>\mu` we can see that the derivate would be negative.

Explanation:

Previous concepts

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The density function for the normal distribution is given by:

`f(x) = (1)/(√(2\pi) \sigma) e^{-(1)/(2) ((x-\mu)/(\sigma))^2}`

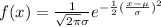
Solution to the problem

Let X the random variable who represent the SAT scores for college bound seniors we know from the info given that
`\mu = 516 , \sigma =116`

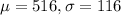
(a) Assuming the date can be modeled by a normal probability density function,find a model for these data.

The model on this case would be given by:

`f(x) = (1)/(√(2\pi)(116)) e^{-(1)/(2) ((x-516)/(116))^2}`

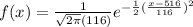
(b) Use a graphing utility to graph the model.Be sure to choose an appropriate viewing window.

We can use the following R code to plot the density function:

> x<-seq(0,1000,by=0.1)

> y=dnorm(x,mean=516,sd=116)

> plot(x,y,main="Density plot")

And the result is on the figure attached

(c) Find the derivative of the model.

For this case we can find the partial derivate respect
`\mu` or
`\sigma` but is much easier find the derivate respect
`\mu`

`(d)/(d \mu) = (1)/(√(2\pi) \sigma) e^{-(1)/(2) ((x-\mu)/(\sigma))^2} * ((\mu-x)/(\sigma)) *((1)/(\sigma))`

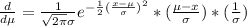
The derivate respect to
`\sigma`

`(d)/(d \sigma^2)= -(1)/(2 √(2\pi) \sigma^2) e^{-(1)/(2) ((x-\mu)/(\sigma))^2} + (1)/(√(2\pi)\sigma) e^{-(1)/(2) ((x-\mu)/(\sigma))^2}((\mu-x)/(\sigma)) *(-(x-\mu)/(\sigma^2))`

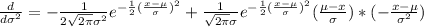
(d) show that f' > 0 for x < µ and f' < 0 for x > µ.

For this case if we analyze the function obtained for
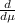`(d)/(d\mu)` we can see that if we replace any value of
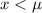`x < \mu` , and we know that
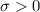`\sigma>0` always then we will have a positive value since we just need to analyze this part of the expression :

`(\mu-x)/(\sigma)`

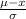
And when we replace any value
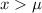`x>\mu` we can see that the derivate would be negative.