Question

Analyze a graph In Exercise,analyze and sketch the graph of the function.Label any relative extrema, points of inflation,and asymptotes.

f(x) = x2e - x

Answer 1

Explanation:

Given is a function f(x)

`f(x) = x^2 e^(-x)`

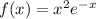
We have to analyse and sketch the grapy

X intercept : Put y =0, we get x =0 or infinity

Y intercept: Put x =0 , we get y =0

The function being product of a square divided by power of e can never be negative. Hence range is (0,infty)

Since when y=0 x has a solution as infinity, x axis is asymptote

`f'(x) = (2x -x^2)e^(-x)`

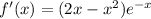
f' becomes 0 when x = 0 or 2

`f''(x) = (-2x +x^2+2-2x)e^(-x)`

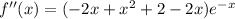
f"(x) >0 for x=2 and <0 for x=0

Hence maxima at x=2 and minima at x=0

Graph is attached below