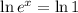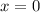Question

Solving Equations In Exercise,solve the equation for
ex = 1

Answer 1

The solution for x is
`x = 0`

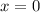
Explanation:

The first step to solve this equation is placing everything with the exponential to one side of the equality, and everything without the exponential to the other side. So

`e^(x) = 1`

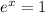
The first part is already how we want, so ok.

Now, we need to know that the ln and the exponential are inverse functions. This means that, for example,
`\ln{e^(x)} = x`.

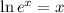So, applying ln to both sides

`\ln{e^(x)} = ln(1)`

`x = 0`