Question

Finding second Derivatives In Exercise,find the second derivate.
f(x) = (3 + 2x)e - 3x

Answer 1

the question is incomplete, the complete question is "Finding second Derivatives In Exercise,find the second derivate.

`f(x)=(3+2x)e^(-3x)`"

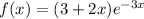answer:
`(df(x)^(2))/(dx^(2))=(15+18x)e^(-3x)\\`,

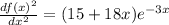Explanation:

To determine the second derivative, we differentiate twice.

for the first differentiation, we use the product rule approach. i.e

`f(x)=u(x)v(x)\\(df(x))/(dx)=u(x)(dv(x))/(dx)+ v(x)(du(x))/(dx)\\`

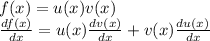
from
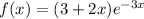`f(x)=(3+2x)e^(-3x)` if w assign

u(x)=(3+2x) and the derivative,
`(du(x))/(dx)=2`

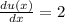
also
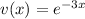`v(x)=e^(-3x)` and the derivative
`(dv(x))/(dx)=-3e^(-3x)`.

If we substitute values we arrive at

`(df(x))/(dx)=(3+2x)(-3e^(-3x))+2e^(-3x)\\(df(x))/(dx)=(-9-6x)e^(-3x)+2e^(-3x)\\(df(x))/(dx)=(-9-6x+2)e^(-3x)\\(df(x))/(dx)=-(7+6x)e^(-3x)\\`,

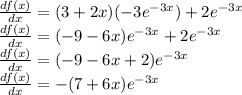Now to determine the second derivative we use the product rule again

this time, u(x)=(7+6x) and the derivative,
`(du(x))/(dx)=6`

also
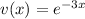`v(x)=e^(-3x)` and the derivative
`(dv(x))/(dx)=-3e^(-3x)`.

If we substitute values we arrive at

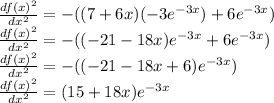`(df(x)^(2))/(dx^(2))=-((7+6x)(-3e^(-3x))+6e^(-3x))\\(df(x)^(2))/(dx^(2))=-((-21-18x)e^(-3x)+6e^(-3x))\\(df(x)^(2))/(dx^(2))=-((-21-18x+6)e^(-3x))\\(df(x)^(2))/(dx^(2))=(15+18x)e^(-3x)\\`,