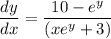Answer:
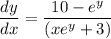
Explanation:
Given:
The implicit equation is given as:
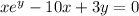
In implicit differentiation, we treat 'y' as a function of 'x' and differentiate both sides of the equation with respect to 'x' and then collect all the
 together and finally solve for
together and finally solve for
 .
.
So, differentiating both sides of the above equation with respect to 'x'. This gives,

Therefore, the derivative
 implicitly is:
implicitly is: