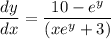Question

Finding Derivatives Implicity In Exercise,Find dy/dx implicity.
xey - 10x + 3y = 0

Answer 1

`(dy)/(dx)=(10-e^y)/((xe^y+3))`

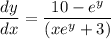
Explanation:

Given:

The implicit equation is given as:

`xe^y-10x+3y=0`

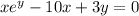
In implicit differentiation, we treat 'y' as a function of 'x' and differentiate both sides of the equation with respect to 'x' and then collect all the
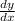`(dy)/(dx)` together and finally solve for
`(dy)/(dx)`.

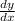So, differentiating both sides of the above equation with respect to 'x'. This gives,

`(d)/(dx)(xe^y-10x+3y)=(d)/(dx)(0)\\\\(d)/(dx)(xe^y)+(d)/(dx)(-10x)+(d)/(dx)(3y)=0\\\\\textrm{Using product rule, (uv)' = uv' + vu'}\\\\(x\cdot e^y\cdot (dy)/(dx)+e^y\cdot 1)-10\cdot1+3(dy)/(dx)=0\\\\(dy)/(dx)(xe^y)+e^y-10+(dy)/(dx)(3)=0\\\\\textrm{Grouping}\ (dy)/(dx)\textrm{ terms together}\\\\(dy)/(dx)(xe^y+3)+e^y-10=0\\\\(dy)/(dx)(xe^y+3)=10-e^y\\\\(dy)/(dx)=(10-e^y)/((xe^y+3))`

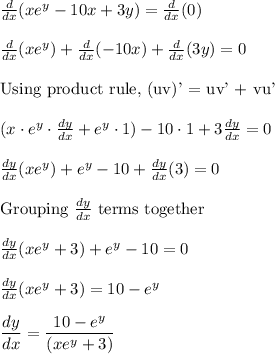
Therefore, the derivative
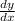`(dy)/(dx)` implicitly is:

`(dy)/(dx)=(10-e^y)/((xe^y+3))`