Answer:
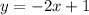
this is the equation of the tangent line to the curve at the point (0,1)
Explanation:
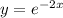
to find the tangent line we need to find the curve's derivative. using
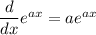 , we'll find dy/dx.
, we'll find dy/dx.
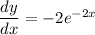
^ this is the equation of the slope of the curve. By finding the slope of the curve at (0,1) we'll also be finding the slope of the tangent to the curve at (0,1).
at (0,1) x = 0. we'll use that in dy/dx
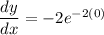
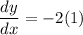
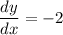
this is the slope of the tangent at point (0,1)
we'll use the general equation of the line formula to find the equation of tangent.
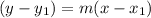
here m is the slope, i.e. m = -2, and (x1,y1)=(0,1)
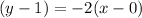
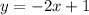
this is the equation of the tangent line at the point (0,1)