Answer:
the question is incomplete, the complete question is "find the derivative of the function
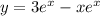 "
"
answer:
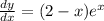 .
.
Explanation:
From the equation,
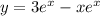 , we approach the question using the differentiation of a product and differentiation of a sum simultaneously,
, we approach the question using the differentiation of a product and differentiation of a sum simultaneously,
the differentiation of a sum is express as
f(x)=u(x)+v(x)+.....w(x) then
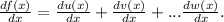
For the differentiation of a product we have
f(x)=u(x)v(x), then
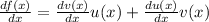
hence if we go by the formula we arrive at
for
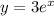
let u(x)=3 hence du/dx=0 and
 and
and
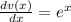
hence
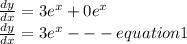
Also for
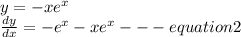 .
.
if we add equation 1 and equation 2 we arrive at
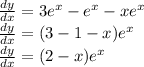 .
.