Question

Finding an Equation of a tangent Line in Exercise, find an equation of the tangent line to the graph of the function at the given point.

y = x/e^2x , (1, 1/e^2)

Answer 1

`y=-(x)/(e^(2))+(2)/(e^(2))\\`

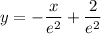
this is the equation of the tangent line to the curve from the point (1, 1/e^2)

Explanation:

`y=(x)/(e^(2x))`

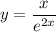
to find the tangent line we need to find the curve's derivative.

we'll be using the quotient formula:
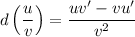`d\left((u)/(v)\right) = (uv'-vu')/(v^2)`, here
`u = x\quad , \quad v = e^(2x)`

`(dy)/(dx)=(e^(2x)(1)-x(2e^(2x)))/((e^(2x))^2)`

`(dy)/(dx)=(e^(2x)-2xe^(2x))/((e^(4x)))`

`(dy)/(dx)=(\left(1-2x\right))/( e^(2 x))`

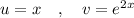
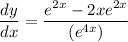
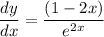
This is the equation of the slope of the curve. By finding the slope of the curve at (1, 1/e^2) we'll also be finding the slope of the tangent to the curve at (1, 1/e^2).

the x-coordinate is 1, so using x =1

`(dy)/(dx)=(\left(1-2(1)\right))/( e^(2(1)))\\(dy)/(dx)=(-1)/(e^(2))`

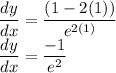
this is the slope of the tangent.

now to find the equation of the line:

`(y-y_1)=m(x-x_1)`

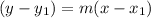
here, m is the slope.

`(y-(1)/(e^(2)))=-(1)/(e^(2))(x-1)\\y=-(x)/(e^(2))+(1)/(e^(2))+(1)/(e^(2))\\`

`y=-(x)/(e^(2))+(2)/(e^(2))\\`

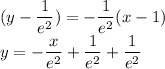
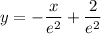
this is the equation of the tangent line to the curve from the point (1, 1/e^2)