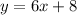Question

Finding an Equation of a tangent Line in Exercise, find an equation of the tangent line to the graph of the function at the given point.

y = (e2x + 1)3,(0 , 8)

Answer 1

Equation of tangent to the line will be
`y=6x+8`

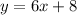
Explanation:

We have given equation
`y=3(e^(2x)+1)=3e^(2x)+3`

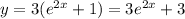
We have to find the equation of tangent passing through the point (0,8)

Slope of the line will be equal to
`(dy)/(dx)=6e^2x+0=6e^(2x)`

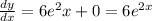
At point (0,8) slope will be
`(dy)/(dx)=6e^(2* 0)=6`

Equation of line is given by

`y-y_1=m(x-x_1)`, here m is slope of the line which is equal to 6 here

So equation of line passing through (0,8)

`y-8=6(x-0)`

`y=6x+8`

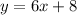
So equation of tangent to the line will be
`y=6x+8`