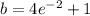Question

Finding an Equation of a tangent Line in Exercise, find an equation of the tangent line to the graph of the function at the given point.

y = e^-2x + x2 , (2 , 1)

Answer 1

`y= -2e^(-2) (x-2) = -2e^(-2) x +(4e^(-2)+1)`

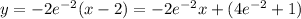
Where the slope is
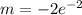`m = -2e^(-2)` and the intercept
`b=4e^(-2)+1`

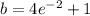
Explanation:

For this case w ehave the following function
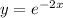`y = e^(-2x)` and a point givn P(2,1)

In order to find an equation of the tangent line to the graph of the function given at the point P first we need to find the derivat eof our original equation.

`(dy)/(dx) =(d)/(dx) (e^(-2x))`

`(dy)/(dx) = -2 e^(-2x)`

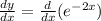
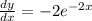
And this value represent the slope for our tangent line at the given point, we can replace the value of x and we got:

`m = (dy)/(dx) = -2 e^(-2(1))= -2e^(-2)=-0.2708`

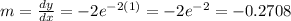
Now the general equation for the tangent line is given by:

`y -y_0 = m (x-x_0)`

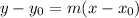
And for this case
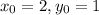`x_0 = 2, y_0 = 1` and if we replace we got:

`y -1 = -2e^(-2) (x-2) = -2e^(-2) x +4e^(-2)`

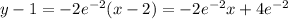
And if we simplify we got:

`y= -2e^(-2) (x-2) = -2e^(-2) x +(4e^(-2)+1)`

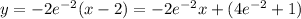
Where the slope is
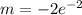`m = -2e^(-2)` and the intercept
`b=4e^(-2)+1`