Question

For p = $3000, r = 3.5%,and t = 5 years, Find the balance in an account When interest is compounded (a) quarterly, (b) monthly,and (c) continuously.

Answer 1

Explanation:

a) P = 3000

It was compounded quarterly. This means that it was compounded 4 times in a year. So

n = 4

The rate at which the principal was compounded is 3.5%. So

r = 3.5/100 = 0.035

It was compounded for just 5 years. So

t = 5

The formula for compound interest is

A = P(1+r/n)^nt

A = total amount in the account at the end of t years. Therefore

A = 3000 (1+0.035/4)^4×5

A = $3571

b) It was compounded monthly. This means that it was compounded 12 times in a year. So

n = 12

Therefore,

A = 3000 (1+0.035/12)^12×5

A = $3572.88

c) The formula for continuously compounded interest is

A = Pe (r x t)

where

e = 2.7183.

Therefore

A = 3000 × 2.7183^(0.035 × 5)

A = $3573.7

Answer 2

a) $3,571.02

b) $3,572.9

c) $3,573.74

Explanation:

Data provided in the question:

p = $3000,

r = 3.5%,

t = 5 years

a) quarterly

number of periods in a year, n = 4

Interest rate per period = 3.5% ÷ 4 = 0.875%

Now,

`A = p* \left( 1 + (r)/(n) \right)^{\Large{n \cdot t}}`

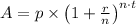
A = total amount

n = number of times compounded per year

on substituting the respective values, we get

A = 3000 ×
`\left( 1 + ( 0.035 )/( 4 ) \right)^{\Large{ 4 \cdot 5 }}`

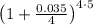
A = 3000 × [/tex]\cdot { 1.00875 } ^ { 20 }[/tex]

A = 3000 × 1.19034

A = $3,571.02

b) monthly

number of periods in a year, n = 12

Now,

A =
`p* \left( 1 + (r)/(n) \right)^{\Large{n \cdot t}}`

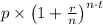
on substituting the respective values, we get

A = 3000 ×
`\left( 1 + ( 0.035 )/( 12 ) \right)^{\Large{ 12 \cdot 5 }}`

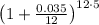
A = 3000 × [/tex]\cdot { 1.002917} ^ { 60 }[/tex]

A = 3000 × 1.190967

A = $3,572.9

c) continuously

A =
`pe^(r* t)`

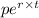
on substituting the respective values, we get

A = 3,000 ×
`e^(0.035* 5)`

or

A = 3,000 ×
`e^(0.175)`

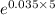
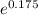
or

A = 3,000 × 1.1912

or

A = $3,573.74