Question

After t years, the remaining mass y (in grams) of an initial mass of 35 grams of a radioactive element whose half- life is 80 years is given by

y = 35(1/2)^t/80 , t ≥ 0.
How much of the initial mass remains after 50 years?

Answer 1

Answer: There will be 22.694 grams of initial mass remains after 50 years.

Explanation:

Since we have given that

`y=35((1)/(2))^{(t)/(80)`

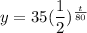
We need to find the quantity of initial mass remains after 50 years.

So, t = 50 years,

We get that

`y=35((1)/(2))^{(50)/(80)}\\\\y=35(0.5)^(0.625)\\\\y=22.694`

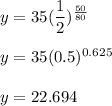
Hence, there will be 22.694 grams of initial mass remains after 50 years.