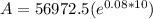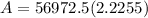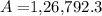Question

The function in Exercise represents the rate of flow of money in dollars per year. Assume a 10-year period at 8% compounded continuously and find the following: (a) the present value; (b) the accumulated amount of money flow at t=10.

f(t)=2000

Answer 1

a)
`P= $56,972.5`

b)
`A=$1,26,792.3`

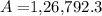
Explanation:

Given Data:

Interest rate=
`r= 0.08` per year

No. of years=
`t=10`

Rate of continuous money flow is given by the function

`f(t)=2000`

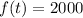
a) to find the present value of money

`P=\int\limits^n_0 {f(t)e^(-rt) } \, dt`

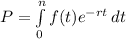
Put f(t)=2000 and n=10 years and r=0.08

`P=\int\limits^n_0 {2000e^(-0.08t) } \, dt`

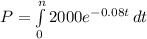
Now integrate

`P= {2000((e^(-0.08t))/(-0.08) )`

`P= -(2000)/(0.08) (e^(-0.08*10)-e^(-0.08*0))`

`P= -(2000)/(0.08) (e^(-0.8)-e^(0))`

`P= -(2000)/(0.08) (0.4493-2.7282)`

`P= -(2000)/(0.08) (-2.2789)`

`P= -25000(-2.2789)`

`P= $56972.5`

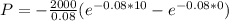
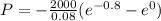
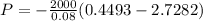
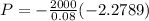
(b) to find the accumulated amount of money at t=10

`A=P(e^(rt) )`

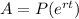
Where P is the present worth already calculated in part a

`A=56972.5(e^(0.08*10) )`

`A=56972.5(e^(0.8) )`

`A=56972.5(2.2255 )`

`A=$1,26,792.3`