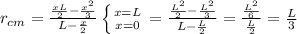Question

A non uniform rod has mass

M
and length
L
. If left end of the rod is placed at
x
=
0
, the mass per unit length of the rod varies according to:
σ
(
x
)
=
b
(
L
−
x
)
, where
b
is a constant to be determined. What is the position of the center of mass of this rod?

1.
5
L
7
2.
L
3
3.
2
L
3
4.
L
2
5
3
L
4
6.
L
4
7.
4
L
5
8.
L
5

Answer 1

`r_(cm) = L/3`

Step-by-step explanation:

Mass: M, Length: L.

`\sigma (x) = b(L-x)`

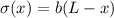
The formula that gives center of mass is

`\vec{r}_(cm) = \frac{m_1\vec{r}_1 + m_2\vec{r}_2 + ...}{m_1 + m_2 + ...} = \frac{\Sigma m_i \vec{r}_i}{\Sigma m_i}`

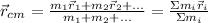
In the case of a non-uniform mass density, this formula converts to

`\vec{r}_(cm) = \frac{\int\limits^L_0 {x\sigma(x)} \, dx }{\int\limits^L_0 {\sigma(x)} \, dx }`

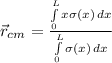
where the denominator is the total mass and the nominator is the mass times position of each point on the rod.

We have to integrate the mass density over the total rod in order to find the total mass. Likewise, we have to integrate the center of mass of each point (xσ(x)) over the total rod. And if we divide the integrated center of mass to the total mass, we find the center of mass of the rod:

`\vec{r}_(cm) = \frac{\int\limits^L_0 {x\sigma(x)} \, dx }{\int\limits^L_0 {\sigma(x)} \, dx } = \frac{\int\limits^L_0 {xb(L-x)} \, dx }{\int\limits^L_0 {b(L-x)} \, dx } = \frac{b\int\limits^L_0{(xL - x^2)} \, dx }{b\int\limits^L_0 {(L-x)} \, dx } = ((x^2L)/(2) - (x^3)/(3))/(Lx - (x^2)/(2))\left \{ {{x=L} \atop {x=0}} \right.`

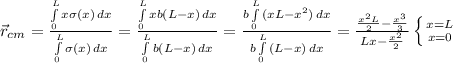
Here x's are cancelled. Otherwise, the denominator would be zero.

`r_(cm) = ((xL)/(2)-(x^2)/(3))/(L-(x)/(2))\left \{ {{x=L} \atop {x=0}} \right. = ((L^2)/(2)-(L^2)/(3))/(L-(L)/(2)) = ((L^2)/(6))/((L)/(2)) = (L)/(3)`