Question

An arrow is shot at a 30 degree angle with the horizontal. it has a velocity of 49 m/s how high will the arrow go? what horizontal distance will the arrow travel? and how long will the arrow be in the air?

Answer 1

That arrow goes 30.59 m high, it travels 211.96 m horizontally and taken 4.99 seconds to land.

Step-by-step explanation:

Consider the vertical motion of ball,

We have equation of motion v = u + at

Initial velocity, u = u sin θ

Final velocity, v = -u sin θ

Acceleration = -g

Substituting

v = u + at

-u sin θ = u sin θ - g t

`t=(2usin\theta )/(g)`

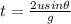
This is the time of flight.

Consider the vertical motion of ball till maximum height,

We have equation of motion v² = u² + 2as

Initial velocity, u = u sin θ

Acceleration, a = -g

Final velocity, v = 0 m/s

Substituting

v² = u² + 2as

0² = u²sin² θ + 2 x -g x H

`H=(u^2sin^2\theta )/(2g)`

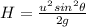
This is the maximum height reached,

Consider the horizontal motion of ball,

Initial velocity, u = u cos θ

Acceleration, a =0 m/s²

Time,
`t=(usin\theta )/(g)`

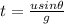
Substituting

s = ut + 0.5 at²

`s=ucos\theta * (2usin\theta )/(g)+0.5* 0* ((2usin\theta )/(g))^2\\\\s=(2u^2sin\theta cos\theta)/(g)\\\\s=(u^2sin2\theta)/(g)`

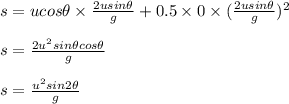
This is the range.

Here u = 49 m/s and θ = 30 degrees

Substituting

`t=(2usin\theta )/(g)=(2* 49* sin30 )/(9.81)=4.99s\\\\H=(u^2sin^2\theta )/(2g)=(49^2* sin^230 )/(2* 9.81)=30.59m\\\\R=(u^2sin2\theta)/(g)=(49^2* sin(2* 30))/(9.81)=211.96m`

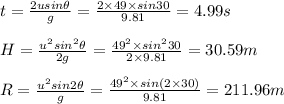
That arrow goes 30.59 m high, it travels 211.96 m horizontally and taken 4.99 seconds to land.