Question

In exercise, find the relative extrema of the function.
f(x) = 1/8x^3 - 2x

Answer 1

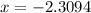`x=-2.3094` is a relative maxima and
`x=2.3094` is a relative minima.

Explanation:

We have been given a function
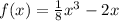`f(x)=(1)/(8)x^3-2x`. We are asked to find the relative extrema of the given function.

First of all, we will find first derivative of the given function as:

`f'(x)=(d)/(dx)((1)/(8)x^3)-(d)/(dx)(2x)`

`f'(x)=3*(1)/(8)x^(3-1)-2*(x^(1-1))`

`f'(x)=(3)/(8)x^(2)-2*(x^0)`

`f'(x)=(3)/(8)x^(2)-2*(1)`

`f'(x)=(3)/(8)x^(2)-2`

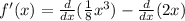
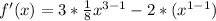
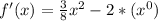
Now, we will find the critical points by equating derivative to 0 as:

`(3)/(8)x^(2)-2=0`

`(3)/(8)x^(2)=2`

`(8)/(3)*(3)/(8)x^(2)=(8)/(3)*2`

`x^(2)=(16)/(3)`

`x=\pm \sqrt{(16)/(3)}`

`x=\pm 2.3094`

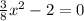
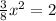
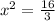
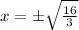
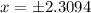
Noe, we will check on which intervals our given function is increasing or decreasing.

`f'(-4)=(3)/(8)(-4)^(2)-2`

`f'(-4)=(3)/(8)(16)-2`

`f'(-4)=3*2-2`

`f'(-4)=4`

`f'(1)=(3)/(8)(1)^(2)-2`

`f'(1)=(3)/(8)-2`

`f'(1)=-1.625`

`f'(4)=(3)/(8)(4)^(2)-2`

`f'(4)=(3)/(8)(16)-2`

`f'(4)=3*2-2`

`f'(4)=4`

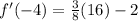
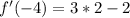
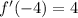
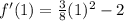
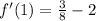
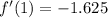
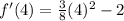
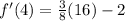
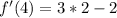
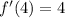
We know that when
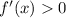`f'(x)>0`, then f is increasing and when
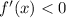`f'(x)<0`, then f is decreasing.

Therefore,
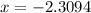`x=-2.3094` is a relative maxima and
`x=2.3094` is a relative minima.