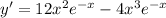Answer: The derivative would be
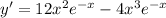
Explanation:
Since we have given that
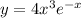
We need to find the derivative of the function:
We will use "Product rule"
f'(x)= derivative of first function × second function + derivative of second function × first function.
As we know that
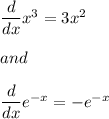
Now, we will get that

Hence, the derivative would be