Question

Differentiating Exponential functions In Exercise,find the derivative of the function. See Example 2 and 3.

f(x) = e1/x

Answer 1

`(d)/(dx) (e^{(1)/(x)}) = e^{(1)/(x)} (-(1)/(x^2)) = -\frac{e^{(1)/(x)}}{x^2}`

Explanation:

Assuming the following function
`y = e^{(1)/(x)}` we want to find the derivate of this function.

For this case we need to apply the chain rule given by the following formula:

`(df(u))/(dx) = (df)/(du) (du)/(dx)`

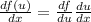
On this case our function is
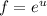`f = e^u` and our value for u is
`u = (1)/(x)`

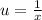
If we appply this rule we got this:

`(df(u))/(dx) = (d)/(du) (e^u) (d)/(dx) ((1)/(x))`

`(df(u))/(dx) = e^u (-(1)/(x^2))`

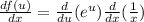
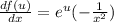
And now w can substitute
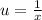`u = (1)/(x)` and we got:

`(d)/(dx) (e^{(1)/(x)}) = e^{(1)/(x)} (-(1)/(x^2)) = -\frac{e^{(1)/(x)}}{x^2}`