Question

How many roots of the polynomial 30x^4 + 7x^3-125x^2-54x+72 have absolute value greater than 1?

Answer 1

There are 3 roots of the given polynomial that have absolute value greater than 1.

Explanation:

We are given the polynomial:

`p(x) = 30x^4 + 7x^3-125x^2-54x+72`

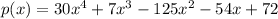
We can factorize the given polynomial as:

`p(x) = 30x^4 + 7x^3-125x^2-54x+72\\=(x-2)(2x+3)(5x-3)(3x+4)=0`

`\text{Solving for}\\(x-2) = 0\\x = 2\\|x| = 2 > 1`

`\text{Solving for}\\(2x+3) = 0\\x = (-3)/(2)\\\bigg|(-3)/(2)\bigg| = (3)/(2) > 1`

`\text{Solving for}\\(5x-3) = 0\\x = (3)/(5)\\\bigg|(3)/(5)\bigg| = (3)/(5) < 1`

`\text{Solving for}\\(3x+4) = 0\\x = (-4)/(3)\\\bigg|(-4)/(3)\bigg| = (4)/(3) > 1`

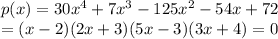
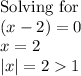
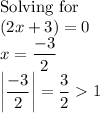
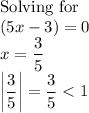
Thus, there are 3 roots of the given polynomial that have absolute value greater than 1.