In Exercise,factor the expression. x^2e^x - 1/2e^x

Question

asked Jun 23, 2021 130k views

1 Answer

Saadiq · Answer 1 · 2021-06-28T17:04:58+0000

Answer:

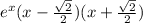
e^x (x- (√(2))/(2)) (x+(√(2))/(2))

Explanation:

For this case we have the following expression:

x^2 e^x - (1)/(2)e^x

And we want to factorize this, the first step on this case would be taking common factor
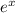e^x and we got this:

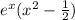
e^x (x^2 -(1)/(2))

Now we can apply this case of factorization called difference of perfect squares:

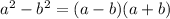
a^2 -b^2 = (a-b)(a+b)

For this case
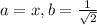
a = x , b = (1)/(√(2))

And if we apply this we got:

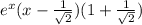
e^x (x- (1)/(√(2)))(1+ (1)/(√(2)))

Now we can rationalize the expression with the square root on the denominator like this:

(1)/(√(2)) * (√(2))/(√(2)) = (√(2))/(2)

And if we replace this we got:

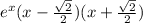
e^x (x- (√(2))/(2)) (x+(√(2))/(2))

And that would be our final expression.