Answer:
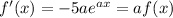 , where a be a constant.
, where a be a constant.
Explanation:
Note: The given functions is a constant function because variable term is missing.
Consider the given function is
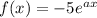
where a be a constant.
We need to find the derivative of the function.
Differentiate with respect to x.
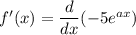
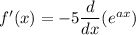
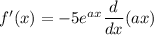
![[\because (d)/(dx)(e^x)=e^x]](https://img.qammunity.org/2021/formulas/mathematics/college/4g6d81on9zqxwpob4xmi1wzxn9nly20h8m.png)
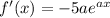
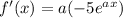
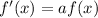
Therefore, the derivative of the function is
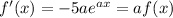 .
.