Answer:
Explanation:
Given that demand function for a product is modeled by
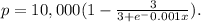
where p = price in dollars and
x= units demanded
a) When x=1000, we substitute 1000 for x
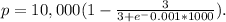
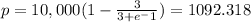
i.e. price is 1092.32 dollars
b) X = 1500
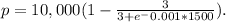
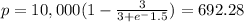
i.e. price is 692.28 dollars
c) When x increases without bound exponent with negative power becomes 0 making price = 10000(1-3/3) =0