Question

Demand the demand function for a product is modeled by

p = 10,000(1- 3/3+e^-0.001x).
Find the price P (in dollars) of the product when the quantity demanded is (a) x = 1000 units and (b) x = 1500units.(c) what is the limit of the price as x increase without bound?

Answer 1

Explanation:

Given that demand function for a product is modeled by

`p = 10,000(1- (3)/(3+e^-0.001x) ).`

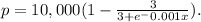
where p = price in dollars and

x= units demanded

a) When x=1000, we substitute 1000 for x

`p = 10,000(1- (3)/(3+e^-0.001*1000) ).`

`p = 10,000(1- (3)/(3+e^-1) )=1092.318`

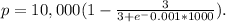
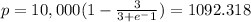
i.e. price is 1092.32 dollars

b) X = 1500

`p = 10,000(1- (3)/(3+e^-0.001*1500) ).`

`p = 10,000(1- (3)/(3+e^-1.5) )=692.28`

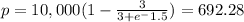
i.e. price is 692.28 dollars

c) When x increases without bound exponent with negative power becomes 0 making price = 10000(1-3/3) =0