Answer:
a)
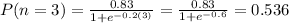
b)
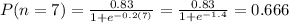
c)
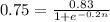
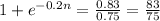
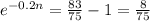
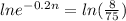
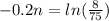
And then if we solve for t we got:
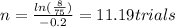
d) If we find the limit when n tend to infinity for the function we have this:
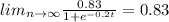
So then the number of correct responses have a limit and is 0.83 as n increases without bound.
Explanation:
For this case we have the following expression for the proportion of correct responses after n trials:
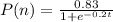
Part a
For this case we just need to replace the value of n=3 in order to see what we got:
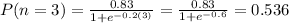
So the number of correct reponses after 3 trials is approximately 0.536.
Part b
For this case we just need to replace the value of n=7 in order to see what we got:
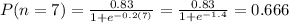
So the number of correct responses after 7 weeks is approximately 0.666.
Part c
For this case we want to solve the following equation:
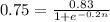
And we can rewrite this expression like this:
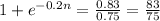
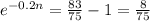
Now we can apply natural log on both sides and we got:
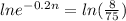
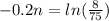
And then if we solve for t we got:
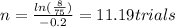
And we can see this on the plot attached.
Part d
If we find the limit when n tend to infinity for the function we have this:
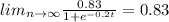
So then the number of correct responses have a limit and is 0.83 as n increases without bound.