Question

Indicate the sum of the terms in each of the following examples, and simplify the result by combining like terms:

10r2, −6r, +5s, −8r, +2s, −5r2, −4s What is the value of this expression for r=1, s=3

Answer 1

The sum of the terms is equal to
`5r^2-14r+3s`.

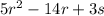The value of the sum at
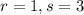`r=1,s=3` is 0.

Explanation:

Given:

The terms that are given are:

`10r^2, -6r, +5s, -8r, +2s, -5r^2, -4s`

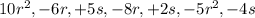
The sum of the terms is the addition of the given terms and is given as:

`=10r^2+ (-6r)+5s+ (-8r)+2s + (-5r^2) + (-4s)`

`=10r^2-6r+5s-8r+2s-5r^2-4s`

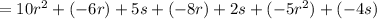
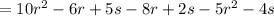
Now, combining like terms. Like terms means that are of the same type are grouped together. There are 3 different terms here 'r²', 'r' and 's'.

The terms containing 'r²' are:
`10r^2, -5r^2`

The terms containing 'r' are:
`-8r, -6r`

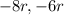
The terms containing 's' are:
`5s, 2s, -4s`

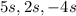
Now, combining the like terms, we get:

`=(10r^2-5r^2)+(-8r-6r)+(5s + 2s -4s)`

`=(10-5)r^2+(-8-6)r+(5+2-4)s`

`=5r^2+(-14)r+3s`

`=5r^2-14r+3s`

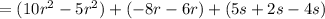
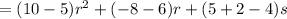
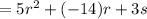
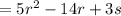
Therefore, the final expression is equal to:

`=5r^2-14r+3s`

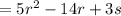
Now, plug in
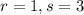`r=1,s=3`. This gives,

`=5(1)^2-14(1)+3(3)`

`=5* 1-14+9`

`=5-14+9`

`=0`

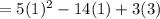
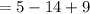
Therefore, the value of the sum of all the terms at
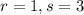`r=1,s=3` is 0.