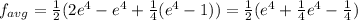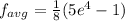Answer:
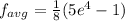
Explanation:
We are given that a function
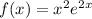
We have to find the average value of function on the given interval [0,2]
Average value of function on interval [a,b] is given by
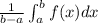
Using the formula
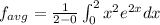
By Parts integration formula
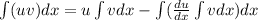
u=
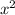 and v=
and v=
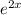
Apply by parts integration
![f_(avg)=(1)/(2-0)([(x^2e^(2x))/(2)]^(2)_(0)-\int_(0)^(2)(2x* (e^(2x))/(2)dx)](https://img.qammunity.org/2021/formulas/mathematics/college/8z7miatkd7sj3b2yit5ndkq01yg3p9swqx.png)
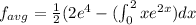
![f_(avg)=(1)/(2)(2e^4-0-([(xe^(2x))/(2)]^(2)-(1)/(4)[e^(2x)]^(2)_(0)))](https://img.qammunity.org/2021/formulas/mathematics/college/9930f0o90utywxqfrmhejoltpe99wfx88y.png)