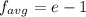Answer:
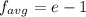
Explanation:
We are given that a function

We have to find the average value of function on the given interval [0,7]
Average value of function on interval [a,b] is given by
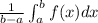
Using the formula
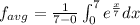
![f_(avg)=(1)/(7)[e^{(x)/(7)}* 7)]^(7)_(0)](https://img.qammunity.org/2021/formulas/mathematics/college/granfa3metbmssxouysw692e5ljoyinh4f.png)
By using the formula
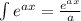

Because
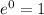
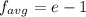
Hence, the average value of function on interval [0,7]