Question

Finding Account Balances In Exercise,complete the table to determine the table A for P dollars invested at rate r for t years,compounded n times per year .see Example 3.

n 1 2 4 12 365 continuous compounding
A
p = $2500,r = 5%,t = 40 years

Answer 1

`n=1, A=17599.97`

`n=2, A=18023.91`

`n=4, A=18245.052`

`n=12, A=18395.45`

`n=365, A=18470.02`

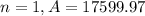
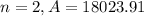
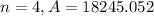
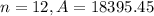
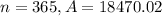
Explanation:

P=$2500

r = 5%

t = 40 years

A= ? for n= 1, 2, 4, 12, 365

Continuous compounding is given by

`A=P(1+(r)/(n) )^(nt)`

`A=2500(1+(0.05)/(n) )^(n*40)`

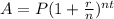
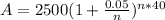
For n=1

`A=2500(1+(0.05)/(1) )^(1*40)=2500(7.039988) =17599.97`

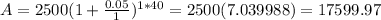
For n=2

`A=2500(1+(0.05)/(2) )^(2*40)=2500(7.209567) =18023.91`

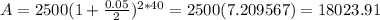
For n=4

`A=2500(1+(0.05)/(4) )^(4*40)=2500(7.2980208) =18245.052`

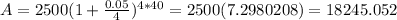
For n=12

`A=2500(1+(0.05)/(12) )^(12*40)=2500(7.3581828) =18395.45`

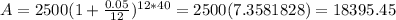
For n=365

`A=2500(1+(0.05)/(365) )^(365*40)=2500(7.3880115) =18470.02`

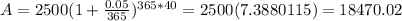
As the value of n keeps on increasing the value of A is coming to a steady value thus we approximate this by using exponential function

`A=Pe^(rt)`

`A=2500e^(0.05*40)=18472.64`

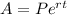
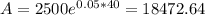
As you can see it is almost equal to our answer calculated earlier for n=365