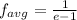Question

Find the average value of the function on the given interval.
f(x)=2 ln x; [1,e]

Answer 1

`f_(avg)=(1)/(e-1)`

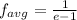
Explanation:

We are given that a function

`f(x)=2lnx`

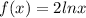
We have to find the average value of function on the given interval [1,e]

Average value of function on interval [a,b] is given by

`(1)/(b-a)\int_(a)^(b)f(x)dx`

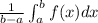
Using the formula

`f_(avg)=(1)/(e-1)\int_(1)^(e)lnx dx`

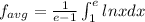
By Parts integration formula

`\int(uv)dx=u\int vdx-\int((du)/(dx)\int vdx)dx`

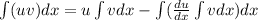
u=ln x and v=dx

Apply by parts integration

`f_(avg)=(1)/(e-1)([xlnx]^(e)_(1)-\int_(1)^(e)((1)/(x)* xdx))`

`f_(avg)=(1)/(e-1)(elne-ln1-[x]^(e)_(1))`

`f_(avg)=(1)/(e-1)(e-0-e+1)=(1)/(e-1)`

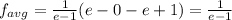
By using property lne=1,ln 1=0

`f_(avg)=(1)/(e-1)`