Question

A 30-meter high building sits on top of a hill. The angles of elevation of the top and bottom of the building from the same spot at the base of the hill are measured to be 55 degrees and 50 degrees. How high is the hill to the nearest meter?

Answer 1

A 30-meter high building sits on top of a 151.52 meter high hill.

Step-by-step explanation:

According to the given data, we can draw a figure (Please refer the attachment below)

Building's height = 30 meter

Angle of elevation from a spot to the top of the building = 55 degrees

Angle of elevation from the spot to the top of the building = 50 degrees

To find the height of the hill, we need to use the formula,

`tan \,\theta = (opposite \,side)/(adjacent \,side)`

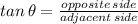
then,
`tan \,50 = (h)/(x)`

`\Rightarrow x = (h)/(tan 50)`

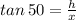
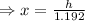`\Rightarrow x = (h)/(1.192)` .... (1)

Similarly,
`tan \,55 = (30+h)/(x)`

`\Rightarrow x = (30+h)/(tan 55)`

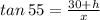
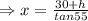
`\Rightarrow x = (30+h)/(1.192)` .... (2)

(1) = (2) becomes

`(h)/(1.192) = (30+h)/(1.428)`

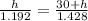
[tex]\Rightarrow [tex] 1.428h = (30 + h)1.192

1.428h = 35.76 + 1.192h

1.428h - 1.192h = 35.76

0.236h = 35.76

h = 151.52 meter

Therefore, the hill highs 151.52 meter.