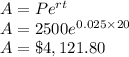Answer:
n = 1, A = $4,096.54
n = 2, A = $4,109.04
n = 4, A = $4,115.39
n = 12, A = $4,119.66
n = 365, A = $4,121.73
Compounded continuously, A = $4,121.80
Explanation:
We are given the following in the question:
P = $2500
r = 2.5% = 0.025
t = 20 years
Formula:
The compound interest is given by
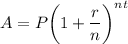
where P is the principal, r is the interest rate, t is the time, n is the nature of compound interest and A is the final amount.
For n = 1
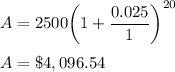
For n = 2
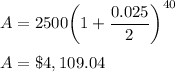
For n = 4
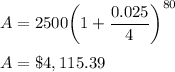
For n = 12
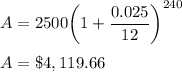
For n = 365
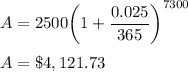
Continuous compounding: