Question

Describe in words the region of R3 reperesented by the equations or inequalities x2+y2=4,z=-1

Answer 1

It represents a circle of radius 2, centered in the origin of the plane xy and transversal to the z-axis in z=-1.

Explanation:

The first thing to notice is that

`x^2+y^2=2^2`

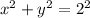
represents a circle of radius 2, with its center in the origin of a plane xy, of cartesians coordinates.

Starting from here, we have to put the coordinate z, to complete the space R³. Then, the cirlce will "live" into the plane xy, where z=-1.

Finally, we have that this region is a circle of radius 2, centered in the origin of the plane xy, and transversal to z=-1.