Question

A club volleyball league allows only the top 5% of athletes who try out to be part of the team. If the team tryout scorecard has a mean of 250 and a standard deviation of 15, which of the following can be used as a minimum qualifying score to join the volleyball league? 13 237 251 274

Answer 1

274

Explanation:

Answer 2

Among the given options, the one which can be used as a minimum qualifying score to join the volleyball league is, 274.

Explanation:

Let the team tryout scorecard is represented by the random variable X.

Now, according to the question,

X
`\sim` Normal (250 , 15)

Let Z =
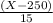`\frac {(X - 250)}{15}` -----------------------(1)

So, Z
`\sim` Normal (0, 1)

According to the question, the bottom 95% in the tryout scorecard are to be eliminated.

Let, P(Z ≤
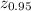`z_(0.95)`) = 0.95

Now, from the inverse standard normal probability table,

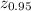`z_(0.95)` = 1.645

So, if we say that

P(X ≤
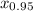`x_(0.95)`) = 0.95, then

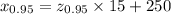`x_(0.95) = z_(0.95) * 15 + 250` --------------[from (1)]

=
`1.645 * 15 + 250`

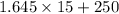
= 274. 675

Hence, from the given options, the answer is, 274.