Answer:
2.13677
Explanation:
Given function in the question:
f(x) =
 ; [1 , 13]
; [1 , 13]
Now,
The average value is calculated as:
⇒
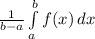
Therefore,
for the given data
a = 1
b = 13
f(x) =

Thus,
average =
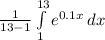
or
average =
![(1)/(12)*[(e^(0.1x))/(0.1)]^(13)_1](https://img.qammunity.org/2021/formulas/mathematics/college/nm9gdm13nh1zz24z59lv0b0g8m01h2qpbe.png)
or
average =
![(1)/(12)*[(e^(0.1(13)))/(0.1)-(e^(0.1(1)))/(0.1)]](https://img.qammunity.org/2021/formulas/mathematics/college/rdi35rq2368lvsi34vb0mkoz4ncb8umoxe.png)
or
Average =
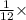 [36.693 - 11.05176]
[36.693 - 11.05176]
Average =
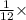 25.64124
25.64124
or
Average = 2.13677