Question

Graphing Natural Exponential Functions In Exercise,sketch the graph of the function.See Example 1.

f(x) = e-x/3

Answer 1

See the graph and explanation below.

Explanation:

For this case we have the following function:

`f(x) = e^{-(x)/(3)}`

We can calculate some points in order to see the tendency of the graph, we can select a set of points for example
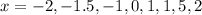`x =-2,-1.5,-1,0,1,1,5,2` and we can calculate the values for f(x) like this

x=-2

`f(x=-2) =e^{-(-2)/(3)}= e^{(2)/(3)}=1.948`

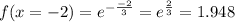
x=-1.5

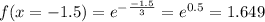
`f(x=-1.5) =e^{-(-1.5)/(3)}= e^(0.5)=1.649`

x=-1

`f(x=-1) =e^{-(-1)/(3)}= e^{(1)/(3)}=1.396`

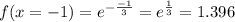
x=0

`f(x=0) =e^{-(0)/(3)}= e^(0)=1`

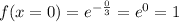
This point correspond to the y intercept.

x=1

`f(x=1) =e^{-(1)/(3)}=0.717`

x=2

`f(x=2) =e^{-(2)/(3)}=0.513`

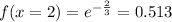
We don't have x intercepts for this case since the function never crosses the x axis.

And then we can see the plot on the figure attached.