Answer:
First Option is correct.
(x+2)(x+3)(x-4)
Explanation:
Given:
The given factor is.
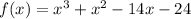
We need to find the factors of given factor.
Solution:
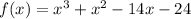
Substitute (-4x-10x) in the place of -14x
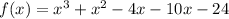
Rearrange the equation:
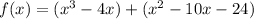
Now we factorised the above equation.
The factors of
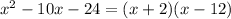
Now we substitute (x+2)(x-12) in the place of
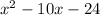
And in the place of
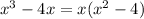
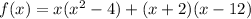
Simplify
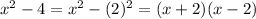
![f(x)=x[(x+2)(x-2)]+(x+2)(x-12)](https://img.qammunity.org/2021/formulas/mathematics/high-school/bpj0apasknt8bt4crlrkd5oeyk18vqkasl.png)
Common factor for above function (x+2)
![f(x)=(x+2)[x(x-2)+(x-12)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/tm832fln10cyxxrk5n608tuhq71hv14kry.png)
Simplify.
![f(x)=(x+2)[x^(2)-2x+x-12]](https://img.qammunity.org/2021/formulas/mathematics/high-school/k5lbn1na0vt37f423iikag7rfwej0n8r4b.png)
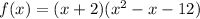
The factor of
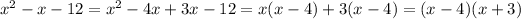
So the factors of the function.
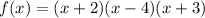
Therefore, the factors of the given function are (x+2)(x-4)(x+3)