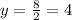Question

In Exercise,find the horizontal asymptote of the graph of the function.
f(x) = 8x^3+2/2x^3+x

Answer 1

Horizontal asymptote of the graph of the function f(x) = (8x^3+2)/(2x^3+x) is at y=4

Explanation:

I attached the graph of the function.

Graphically, it can be seen that the horizontal asymptote of the graph of the function is at y=4. There is also a vertical asymptote at x=0

When denominator's degree (3) is the same as the nominator's degree (3) then the horizontal asymptote is at (numerator's leading coefficient (8) divided by denominator's lading coefficient (2))
`y=(8)/(2)=4`