Answer:
Removable discontinuity at
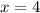 .
.
Explanation:
We have been given a function
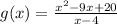 . We are asked to discuss the continuity of the given function.
. We are asked to discuss the continuity of the given function.
We can see our given function is a rational function. We know that a rational function is continuous for all values except those, where denominator is zero.
First of all, we will try to factor the numerator of our given function.
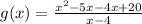

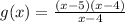
Cancelling out (x-4):
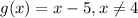
This means that at
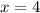 our given function is not defined and it has removable point discontinuity at
our given function is not defined and it has removable point discontinuity at
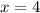 .
.