Question

Find the volume of the solid of revolution formed by rotating about the x--axis the region bounded by the given curves.

f(x)=2-x^2x, y=0.

Answer 1

`V = \pi [4√(2) -(8√(2))/(3) +1.131] =9.478`

Explanation:

For this case we have the following function
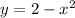`y = 2-x^2` bounded by
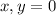`x,y =0`. The area of interest is on the figure attached.

For this case we can calculate the volume using the method of rings. First we can calculate the area like this:

`A(x) = \pi r^2= \pi (2-x^2)^2 = \pi(4-4x^2 + x^4)`

And the volume can be founded with the following formula:

`V= \int_(a)^b A(x) dx`

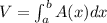
For this case we need to find the intersection point with the x axis, and we can do this:

`2-x^2 = 0`

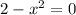
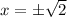`x= \pm √(2)`, but for our case would be just the positive value, So then we can find the volume like this:

`V= \pi \int_(0)^(√(2)) 4 -4x^2 +x^4 dx`

And if we do the integral we got this:

`V = \pi [4x -(4)/(3)x^3 +(x^5)/(5) \Big|_(0)^(√(2))]`

And when we apply the fundamental theorem of calculus we got:

`V = \pi [(4√(2) -(4)/(3) (√(2))^3 +((√(2))^5)/(5)) -(0)]`

`V = \pi [4√(2) -(8√(2))/(3) +1.131] =9.478`