Answer:
The total profit P(x) or the month is
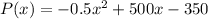 .
.
Explanation:
A company produces x units of a product per month.
The total cost represents by the function C(x).
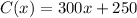
The total revenue represents by the function R(x).
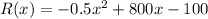
The profit is the difference between revenue and cost.


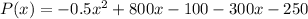
Combine like terms.
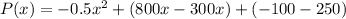
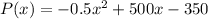
Therefore, the total profit P(x) or the month is
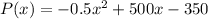 .
.