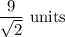Question

Show that the equation represent a sphere, and find its center and radius. 2x2+2y2+2z2=8x-24z+1

Answer 1

Center of sphere = (2, 0, -6)

Radius of sphere =
`(9)/(\sqrt2)\text{ units}`

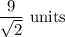
Explanation:

We are given the following in the question:

Equation of sphere:

`2x^2+2y^2+2z^2=8x-24z+1`

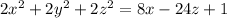
Formula:

The equation of sphere is of the form

`(x-a)^2 + (y-b)^2 + (z-c)^2 = r^2\\\text{where (a,b,c) is the center of sphere and r is the radius of sphere.}`

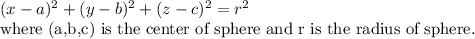
Simplifying the given equation we get,

`2x^2+2y^2+2z^2=8x-24z+1\\\text{Dividing by 2}\\x^2 + y^2 + z^2 = (1)/(2) + 4x - 12z\\\\x^2 -4x + y^2 + z^2+12z = (1)/(2)\\\\\text{Adding 4 and 36 on both sides, we get,}\\\\x^2-4x + 4 +y^2+ z^2+12z + 36 = (1)/(2) + 4+ 36\\\\(x-2)^2 + (y-0)^2 + (z+6)^2 = (81)/(2)\\\\\text{Comparing with the equation of sphere}\\a = 2\\b = 0\\c = -6\\\\r^2 = (81)/(2)\\\\r = \sqrt{(81)/(2)}= (9)/(\sqrt2)`

Center of sphere = (2, 0, -6)

Radius of sphere =
`(9)/(\sqrt2)\text{ units}`