Question

Find the volume of the solid of revolution formed by rotating about the x--axis the region bounded by the given curves.

f(x)=√2x+1, y=0, x=1, x=4.

Answer 1

18 \pi cubic units

Explanation:

Given that a region is bounded by

`f(x)=√2x+1, y=0, x=1, x=4`

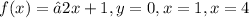
And the region is rotated about x axis.

We can find that here radius would be y value and height would be dx

So volume would be as follows:

If f(x) is rotated about x axis volume

=
`\pi \int\limits^b_a {y^2} \, dx \\=\pi \int\limits^4_1 {2x+1} \, dx\\=\pi *x^2+x  ^4_1\\= \pi*16+4-1-1\\=18\pi`

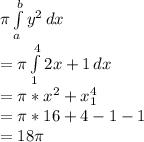
cubic units.