Question

Find an equation of the sphere through the origion and whose center (1,2,3).

Answer 1

x^2 + y^2 + z^2 -2x - 4y - 6y = 0

Explanation:

The equation of a sphere with centre (h, j, k) and radius r is given as

(x - h)^2 + (y - j)^2 + (z - k)^2 = r^2

r =
`√((0 - 1)^2 + (0 - 2)^2 + (0 - 3)^2)`

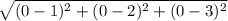
r = sqrt(14)

(x - 1)^2 + (y - 2)^2 + (z - 3)^2 = 14

x^2 - 2x + 1 + y^2 -4y - 4 + z^2 - 6z + 9 = 14

x^2 + y^2 + z^2 -2x - 4y - 6y + 14 = 14

x^2 + y^2 + z^2 -2x - 4y - 6y = 14 -14

x^2 + y^2 + z^2 -2x - 4y - 6y = 0