Answer:
\pi \frac{7}{(11) cubic units
Explanation:
We have to find the volume of the solid of revolution formed by rotating about the x--axis the region bounded by the given curves.
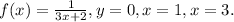
Thus limits for x are 1 and 3
Here
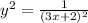
Volume of the solid when f(x) is rotated about x axis from a to b is
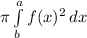
Substitute to get
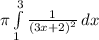
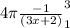
![4\pi \frac{-1}{(11)-\frac{-1}{(4)]() cubic units
cubic units
![\pi \frac{7}{(11)]() cubic units
cubic units